Extreme Learning Machines with Julia

But, this post is not about Deep Learning. Its about a different concept. A network that avoids the murky computation.

Recently, I came across the concept of Reservoir computing, which (in a very simple way) refers to a construct where the input are connected randomly to higher level of abstraction (see it as a hidden layer of higher level) and output can be tapped from those nodes and the training problem reduces to calculating the connection (weights) of tapping nodes to output. This avoids the major bottleneck, iterative tuning of weights of input to higher level.

Well, does this thing even work? Yes, farely well!

There is a concept known as Liquid State Machine, and a relatively better known Echo State Network which is used for training Recurrent Neural Nets. Both of them are based on reservoir computing. On the lines of reservoir computing and very similar in concept is the topic of this post, Extreme Learning Machine.

Extreme learning machine (ELM) is a modification of single layer feedforward network (SLFN) where learning is quite similar to the reservoir topic discussed above.

Given below is a simple SLFN with 3 inputs and 1 output which computes the weighted sum of hidden nodes.

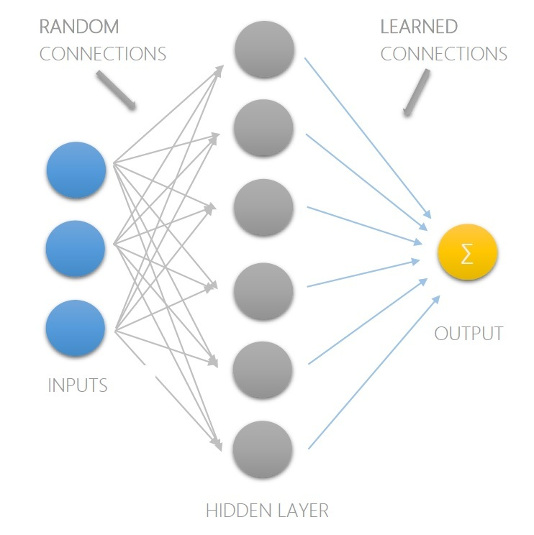
After performing the tedious backpropagation ritual, we are left with the following equation that predicts output from inputs

\[ y = \sum h_i \]

Where \(h_i\) is the activation of \(i^{th}\) hidden neuron computed using

\[ h_i = f(\sum_j (w_{i, j} \times x_j) + b_i) \]

Here, \(f\) is the activation function like sigmoid, tanh etc., \(x\_j\) is the \(j^{th}\) input, \(w\_{i, j}\) is the connection weight from \(j^{th}\) input to \(i^{th}\) hidden neuron and \(b\_i\) is the bias term.

In matrix notation, the process can be represented in the following form

\[ Y = W' \times H \]

Where \(W'\) is the matrix of weights from hidden to output layer while \(H\) is the activation matrix computed using

\[ H = f(W \times X + B) \]

with \(W\) is matrix of weights from input to hidden layer.

Now, being different from usual SLFN, the ELM doesn't tune \(W\) using backprop or any other iterative method, instead \(W\) is randomly generated. This gives us a pool of higher level input abstractions in the hidden layer, out of which, ones fitting to training data can be found by adjusting hidden to output weights by solving a simple matrix equation.

\[ Y = W' \times H \]

Now, given a training data with \(X\) as input and \(Y\) as output, the ELM training process takes the following steps

• Generate \(W\)
• Find \(H\)
• Solve \(Y = W' \times H\) for \(W'\)

The value of \(W'\) can be calculated simply using psuedo (Moore-Penrose) inverse which is usually available as a function that goes by the name pinv most of the scientific computation environment including Matlab and Python's numpy.linalg.

\[ W' = Y \times pinv(H) \]

This inverse can also be computed using regularized inverse for better generalization.

Let's test out the thing.

I happen to believe that we don't need slow languages

Enough to make me try julia.

For python users (for anyone, almost), like me, switching is ridiculously easy and fun. Although still in cradle, julia features nice set of basic libraries for scientific computing. Kinds of DataFrames, Gadfly and IJulia will make you feel at home, whether you are coming from R, scientific Python or Matlab / Octave.

And what you get? Speed, raw and visible! Calling C or fortran from python or R doesn't feel great, especially if you can avoid that.

Coming back to testing. While trying out julia, I coded a simple ELM library. I will be using that, and for comparison with regular NNs, I will be using the ANN library by Eric Chiang. In fact, this post is very much on the lines of a great post by Eric on yhat here.

The problem I will be taking is of a two class classification using the banknote authentication dataset. You can download the dataset and see its attributes here.

Starting off by installing required libraries

Pkg.clone("git://github.com/lepisma/ELM.jl.git");
Pkg.clone("git://github.com/EricChiang/ANN.jl.git");

import ELM, ANN;

Since, both libraries have few functions with same names, so its better to use import rather than using.

Assuming both models give same accuracy, the training of ELM is around 60x faster than ANN! (Which kind of isn't actually surprising since the hidden connections are untouched).