Genetic Algorithms face a ton of criticism. Rather than being a general purpose optimizer, I believe GA is more suited to specific processes with a sensible meaning to what evolution means there.
Being interested in heuristic optimization methods, one thing I notice a lot is confusion in the applicability and efficiency of the methods. Mind you, I am not expert enough to resolve the doubts, but have an opinion which might help in 'some' situations. Ask around for methods to do derivative free optimization and you will stop keeping the count after a while. Specifically in the category of metaheuristics; Cuckoo Search, Genetic Algorithm, Stimulated Annealing, Tabu Search etc. etc. But there is an issue. Give the algorithms a first glance and you will feel they are different. Give them a second glance and many of them will start to cluster in groups. Give a third glance and they are different again!
Earlier, due to the reducible design, I used to consider Genetic Algorithm (GA) as a more general technique as compared to many other evolutionary methods. But then, this might not be what we mean when we want a generally applicable method. A simplistic representation embodying the general principle, like 'mutation in population' for population based heuristics, is what I was looking for instead. GA is, in essence, much more powerful if used in specialized setting with knowledge of the problem. I will go over this proposition later.
Genetic Algorithm faces a lot of criticism. Criticism from researchers are usually constructive. For example there has been a lot of 'debate and work' on the role of crossover in GAs. But I have also seen the users and learners frowning at few of its aspects without going through what it is that GA really does.
1. Fundamental ideas
The main source of inspiration for GA is sexual reproduction. The core ideas including mate selection, gene crossover and mutation are all faithfully (to a certain level of abstraction) incorporated in it. But there are vital differences between the role of sexual reproduction and our needs from GA, a topic covering the meaning of fitness functions and its population aggregate. Let us leave the way fitness is used in traditional GA and focus on the two major operations.
1.1. Mutation
This is simply what every other random search algorithm does. Slight change from the current solution. Using a bit string solution representation like \(0100100\), a simple point mutation along with fitness based selection procedure essentially is the hill climb algorithm. Change bits, evaluate the new positions and shift the population towards the better fitness. This case is stronger with situations including \(N\to\infty\) (larger population size, \(N\)), higher rate of mutation, elite individuals etc.
Mutation coupled with a population and selection procedure results in a nice global optimizer. Even more important is the ease of understanding the word "mutation" with respect to the problem representation. Use bit strings or direct real values or other symbols, mutation means what it means.
1.2. Crossover
In a common representation, a crossover operation swaps sections of solution strings from two mating parents. Now, this needs a little bit of digging. What purpose copying a snippet of gene from parents to children could have? To inherit and move around some specific chunks of functional properties.
A topic of debate among researchers is whether crossover actually has some theoretical advantage and meaning for the problems. Some arguments reduce crossover as a fancy form of mutation, while some arguments support its usage separately.
Without going into the arguments, its better to stick to the fundamentals of crossover and, as a user, exploit its basics. It maintains chunks of properties among the population and across generations.
In GA, you can represent the solution as chromosomes in multiple ways. A common method to represent real number parameters is to use direct value encoding. Let the fitness function simply be \(f(a)\). For crossing over individuals in this form, there are blending and interpolation techniques for numbers. While mating two solutions, \(a_1\) and \(a_2\), a simple \(\alpha\) blending gives
\[ a_3 = \alpha a_1 + (1-\alpha) a_2 \]
Now, here is what the wikipedia page on Differential Evolution (DE) says
DE optimizes a problem by maintaining a population of candidate solutions and creating new candidate solutions by combining existing ones according to its simple formulae, and then keeping whichever candidate solution has the best score or fitness on the optimization problem at hand.
Is there an identity crisis here?
2. Fundamental ideas, again
Look, everything works. Some variations are better and there are theoretical and empirical results backing them up. But then sometimes I feel it is unfair to throw any problem at GA assuming it as a general purpose optimizer. Back to the proposition made in the beginning of the post and the main question of the post. I really like to think the answer to be something on the following lines
GA provides a framework for manipulation of a structure made from symbols to achieve a desired behaviour in decently low time.
Many variations of GA stick to this idea. Genetic Programming is a nice example. Consider following lisp sexpr:
(defun test-function (fn x) "Evaluate negative of slope of function at x" (let ((dx 0.01)) (* -1 (/ (- (fn (+ x dx)) (fn (- x dx))) (* 2 dx)))))
The function is approximating the (-ve of) slope of another function by calculating
\[ -\frac{fn(x + \Delta x) - fn(x - \Delta x)}{2 \times \Delta x} \]
The tree structure of operations has usable chunks which are essential to get the final output. Consider the numerator chunk.
;; ...
(-
(fn (+ x dx))
(fn (- x dx)))
;; ...
This generates an important template for good solutions if you want a quantity like slope. In GA terminology, this template consisting of some form of fixed structure and spaces for variations is called schema. This schema has a fitness associated with it which is the average of fitness of all solutions matching this template. For the above template, the fitness is good since most of the variations around the template will result in some simple operation on the difference of function values. This is better than a case, say, where the template is a sum of function values at two neighbouring points.
The fundamental theorem of GA says that the power of GA comes from increasing the population fraction of schemata with smaller fixed parts and better fitness over generations. The better schemata survive the operations and live on.
Now here is a case. I was using the traditional value encoded form of GA for a global optimization at some point in my undergraduate life. I kept the approach somewhat similar to Matlab's. Value encoding, elite individuals, gaussian mutation, simulated binary crossover and tournament selection. It did whatever it was meant to. But then I started to fiddle around a bit with parameters and switches (whether to use this operation, that selection criteria etc.) and realized that I am doing what can be called cargo cult tuning.
Consider the following fitness surface and value encoding. Considering crossover as extrapolations along some dimension, you can see two kind of results of mating. One better, one worse. That's fine, it happens in real crossovers too.
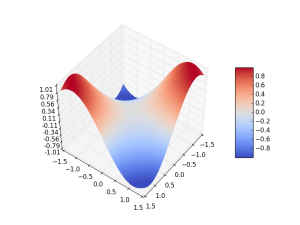
But the point is, user can't seem to understand and extract the power of GA here. What are the schemata getting passed on? Where the crossover points are? More importantly, what can I do to improve performance?
In my opinion, its better to use a method whose knobs (parameters etc.) correspond to the problem in hand and which really pass on the essence of the operations as some connectable effects on the problem. And then judge the algorithm, in case a judgment is to be made.
Last year, Randy Olson blogged about solving a Travelling Salesman Problem (TSP) with Genetic Algorithm. TSP solutions have chunks of continuous paths which can be locally optimal. Debugging makes sense here because the operations are intuitive. Also consider NEAT, which evolves neural network structures. Same idea. Manipulation of symbols and actual implications of crossovers (of chunk of structural trees let's say) etc. Similar is the case with many examples which use Genetic Programming. There are cases where a genetic approach actually provides easier implementation and better results than other methods.
I found this piece of criticism by Steven Skiena on Wikipedia page of GA
[I]t is quite unnatural to model applications in terms of genetic operators like mutation and crossover on bit strings. The pseudobiology adds another level of complexity between you and your problem.
The problem Skiena is addressing is important. The operators are not intuitive at all for general problems and add on the burden of the user. Well, you do get good performance than other methods in different cases. But my opinion is to respect [the full fledged] GA for its help in context of a certain class of problem, not as a go-to general purpose optimizer (for which you would be better started by programming a simple and quick disruptive method).
Your problem can have some allowed set of schemata. For example, if you have a bit string representation of 3-4 parameters, you might like a form of schemata which break the string at the junctions of the numbers for crossovers. Or in some cases you might want to group few bits of strings and evolve them separately. You can try inspirations from speciation. You can create artificial islands. You can try some weird animal group behaviour. They all are good if your problem needs them and the effects are reflected in the evolution of solutions. Otherwise, they are another set of instances of misjudgment of the method.