This is a test notebook for trying out sagemath features
For binary classification, if there are \(n\) component models and the rate of success of each model is \(p\), then the rate of success of a majority voting ensemble can be given using the binomial distribution.
For a simple case of \(n = 21\) and \(p = 0.5\), this means that the ensemble success is given by:
n = 21; c = 2 sum(binom_pmf(0.5).subs(N == n), M, floor(n/c) + 1, n)
0.5
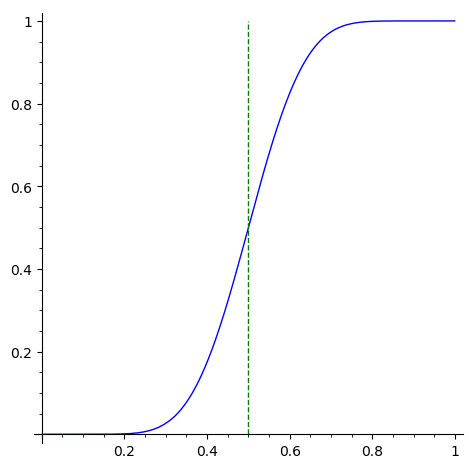
Notice that \(M\) is summed from 11 to 21 which is the zone of majority. A plot of varying \(p\) values follows:
curve = plot(sum(binom_pmf(p).subs(N = n), M, floor(n/c) + 1, n), (p, 0.001, 0.999)) curve + parametric_plot((1/c, x), (x, 0, 1), linestyle="--", color="green")
1. Multiclass
Now assume we have \(c\) classes. The models have a par accuracy of \(1/c\) now. This asks for a question whether a success rate (call it \(q\) as before) greater than \(1 - 1/c\) (or some other value) will result in an ensemble with better performance than any single one.
For a simple case of 3 classes, we have the par error as \(1/3\) and for the ensemble to be right, we need at least \(\lfloor n/3 \rfloor + 1\) models to be right. Meaning the success rate for the ensemble would be:
c = 3 float(sum(binom_pmf(1/c).subs(N == n), M, floor(n/c) + 1, n))
0.3992381153824027
Okay so it does better than the \(1/3\) value.
For 7 classes:
c = 7 float(sum(binom_pmf(1/c).subs(N == n), M, floor(n/c) + 1, n))
0.3523243319568171
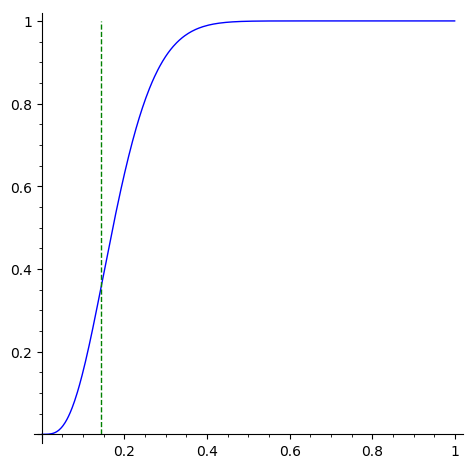
A plot of \(q\) vs ensemble success for 7 classes follows:
curve = plot(sum(binom_pmf(p).subs(N == n), M, floor(n/c) + 1, n), (p, 0.001, 0.999)) curve + parametric_plot((1/c, x), (x, 0, 1), linestyle="--", color="green")
2. Critical p
So you don't need to be above the \(1/c\) threshold in accuracy to gain using a voting ensemble. This means, even a poorer than random classifier will gain here. In general, any \(p\) that makes the following true will be good:
sum(binom_pmf(p), M, floor(N/c + 1), N) > 1/c
sum(p^M*(-p + 1)^(-M + N)*binomial(N, M), M, floor(1/7*N) + 1, N) > (1/7)
Slight increase in \(p\) around this critical value help a lot (as seen from the curves).